El uso de alambre de cobre o aluminio para modificar y fijar la forma de un árbol le permite al entusiasta del bonsái darse cuenta del aspecto plástico de su arte. Cortar y esculpir constituyen el aspecto sustractivo, mientras que solamente la naturaleza puede llevar a cabo operaciones aditivas en el bonsái. Otras técnicas para modelar bonsáis pueden también usarse en conjunción o independientemente al alambrado. Estas técnicas incluyen la de anclar ramas con alambre, colgar pesos de las ramas o e uso de varios tipos de palancas o gatos. El alambrado nos provée de una técnica para lograr la ubicación específica de una rama, por lo que es una de las técnicas mas comúnmente usadas.
Para llevar a cabo esta técnica, un pedazo de alambre del diámetro apropiado y del largo correcto se enrolla alrededor del sistema tronco/rama. Esta serpentina con alambre añade tanto plasticidad como rigidez al sistema. El alambre se deja en el lugar de su colocación por varios meses mientras que el crecimiento bajo esta forma hace permanente la silueta inducida por el alambrado.
ALAMABRES CRUZADOS NO SE PERMITEN EN BONSÁI.
Cuando se alambra un árbol, frecuentemente es deseable alambrar más de una rama. De hecho, no raro alambrar de forma extensiva los árboles, incluyendo en esto todas las ramas primarias y secundarias. Cuando se va a colocar un sistema complejo de alambrado, es necesario evitar el cruce de cualquiera de los alambres por dos razones. La primera de ellas es estética: los alambres cruzados se ven feos e interrumpen flujo natural del montaje. La segunda, los alambres cruzados imprimen una presión desigual al árbol en el lugar de cruce, y si siguen una dirección inversa al alambrado, tendrán muchos lugares de cruce que potencialmente interferirán en la salud del árbol.
UN ÁRBOL PUEDE SER TOTALMENTE ALAMBRADO SIN QUE SE CRUCEN ALAMBRES
Teorema: Todo árbol puede ser alambrado totalmente sin que se cruce ninguno de los alambres utilizados para ello. De vez en vez, algún experto cruzará alambres en alguna demostración pública de su arte, y usted lo escuchará dicsculparse con alguna aseveración referente a que este cruce ocasional no podía ser evitado. Pero esto significa que el demostrador no pensó seriamente sobre el problema o escogió no planear con adelanto suficiente su alambrado. Esto podría no ser un problema grave, pero me parece que si alguien es serio respecto al bonsái, entonces debe tomarse el tiempo para planear adecuadamente su alambrado. Y realmente, planearlo no es del todo complicado si uno enfoca la tarea consistentemente.
PRUEBA DEL TEOREMA DE ALAMBRADO DE WAGNER
El problema se plantea como el de diseñar una configuración completa de alambrado para cualquier árbol de tal forma que ningún alambre se cruce. Esto incluye al tronco y todas sus ramas. Podemos suponer que el grueso del alambre no es significativo porque generalmente este es escogido de tal forma que su grosor sea la tercera parte del tronco o la rama a alambrar. La demostración del teorema nos pondrá de manifiesto que solamente es necesario la utilización simultánea de dos alambres en cualquier tronco o rama para alambrar completamente el árbol.
La prueba es por inducción, primero, sobre el factor de empalme del árbol y segundo, sobre las ramas del árbol. A la vez se mostrará que siempre habrá soluciones múltiples al problema de alambrado.
Los bonsáis generalmente tienen un bajo factor de empalme, pero la prueba siguiente es general y se aplica a cualquier árbol. Primero tomaremos el ejemplo del empalme más simple (binario, factor de empalme de dos) como se muestra en la Figura 1.
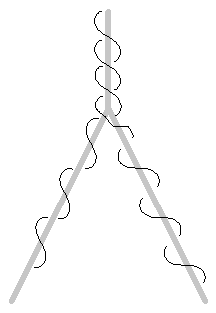
Figura 1: Rama binaria alambrada por el método direct
El enfoque directo ilustrado en la Figura 1 inicia en la raíz de la rama y enrolla el alambre alrededor de una de ellas. Luego inicia de nuevo en la raíz y se enrolla el alambre en la otra rama. De esta forma un número muy grande de ramas pueden ser alambradas, pero la raíz de la rama tiene un número ilimitado de alambres en ella, y por razones prácticas, deseamos limitar el número de alambres en una rama cualquiera. Por ello, usamos el método indirecto mostrado en la Figura 2.
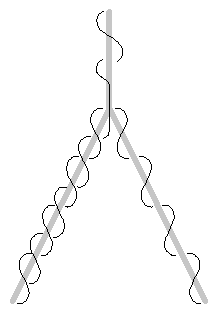
Figura 2: Rama binaria alambrada por el método indirecto
Establecemos los pasos básicos de la inducción con el alambrado indirecto mostrado en la Figura 2: primeramente, alambrar las dos ramas exteriores (las de las hojas) con un pedazo de alambre, para después regresarse a alambrar la raíz de la rama para continuar con una de las ramas exteriores (la izquierda en este caso).
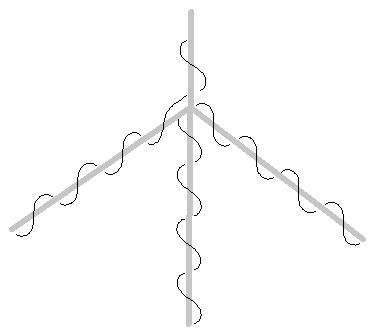
Figura 3: Ramas de tres vías por el método indirecto
Seguidamente, mostraremos por inducción en el número de ramas, que podemos tener un número ilimitado de ramas sin ningún alambre cruzado. La Figura 3 muestra el resultado para tres ramas. En el número impar de empalmes no hay alambres dobles.
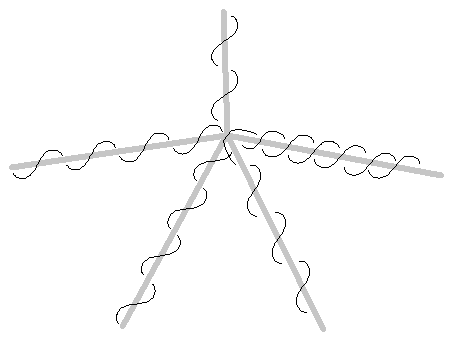
Figura 4: Ramas de cuatro vías por el método indirecto
La Figura 4 nos muestra una configuración de cuatro ramas. Como podrá notarse, en el lugar donde se forma la V, pareciera que los alambres se cruzaran, pero en realidad están cruzando por diferentes lados de la entrepierna (una por atrás y otra en frente). Nótese que hay múltiples posibles soluciones (la rama con alambrado doble puede ser cualquiera de ellas). Esto muestra, por inducción, la técnica general: un número cualquiera de ramas en un empalme particular, puede ser alambrado sin cruzarse. Ahora extenderemos el resultado de las ramas a todo el árbol por inducción. Observe que cualquier rama exterior (las que tiene las hojas), puede tener ella misma un número cualquiera de ramas. Estas sub-ramas de cualquier rama se manejan de forma similar a la rama misma. Esto completa la prueba. Adicionalmente a las múltiples soluciones que se resaltaron anteriormente, el número total de soluciones se duplica permitiendo el alambrado simétrico derecha-izquierda. Por lo tanto, el número total de configuraciones de alambrados es al menos, dos veces el factor de empalme mínimo.
Wiring Bonsai.– Copyright 2001 by Dai Ichi Bonsai Kai and Rick Wagner, all rights reserved.
This page created June 27, 2000, last updated Jan. 22, 2001.
(Traducción al español de Jesús Felipe Rodríguez Romero. Tijuana Baja California, México. Marzo de 2007. http://www.arboleschaparritos.org/)
